Der erste Sieger eines neuen Projekts lautet Mika Schonhoff. Er löste das Problem des Monats als schnellster. Auch andere Schülerinnen und Schüler versuchten ihr Glück, konnten das Problem allerdings nicht vollständig korrekt lösen.

Die Lösungen zu allen vier Teilaufgaben sind hier (Problem des Monats_Februar 2019_Lösungen ) zu finden. Neben Schonhoff hatte vor allem Fachobmann Jürgen Herbrüggen die Aufgaben gelöst. Sehr elegant und auch sehr einfach löste er Aufgabe 4. Auch in Aufgabe 2 wich sein Lösungsweg von dem von Schonhoff ab. Beide hatten die Aufgabe allerdings vollständig richtig. Da der Wettbewerb nur für Schülerinnen und Schüler zugelassen ist, gewann Schonhoff. Natürlich sind auch alle Kolleginnen und Kollegen herzlich eingeladen mitzurätseln und mitzuknobeln an dem neuen Problem, das unten abgedruckt ist und aus der Landesrunde der diesjährigen Mathematik-Olympiade stammt.

In diesem Monat ist das Problem etwas einfacher (aber nicht einfach) gestrickt. Die erste vollständig korrekte Lösung gewinnt.

Aufgabe für den Monat März:

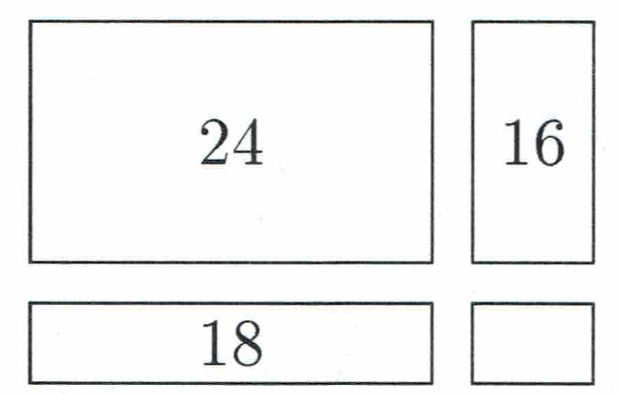
Ein rechteckiges Blatt wird durch zwei Schnitte in vier Rechtecke zerlegt (siehe nebenstehende, nicht maßstabsgerechte Abbildung). Die Seitenlängen der einzelnen Rechtecke seien jeweils ganzzahlig.

(a) Die eingetragenen Zahlen geben jeweils den Umfang der Rechtecke an. Ermittele alle Möglichkeiten für den Umfang des vierten Rechtecks.

(b) Die eingetragenen Zahlen geben jetzt jeweils den Flächeninhalt der Rechtecke an. Ermittle alle Möglichkeiten für den Flächeninhalt des vierten Rechtecks.

Bei der Ehrung zum erstem Problem des Monats: Fachobmann Jürgen Herbrüggen, Mathematik-AG-Leiter Martin Glosemeyer, Problemlöser Mika Schonhoff und Schulleiter Manfred Heuer

Autor: Martin Glosemeyer

Bild: Jaira Hibbel